Modeling a system - An Electrical RC circuit
 |
The circuit above consists of a resistor and capacitor in series. The input variable to the system is the voltage applied, V. There are a couple of output variables from this system that we can measure. One is the charge on the capacitor and the other is the voltage across the capacitor which, from electronics, is defined as the charge on the capacitor divided by the capacitance; i.e. the two variables are related to each other.
Option 1 – Output is charge on the capacitor
Apply the following equation:
In - Out = Accumulation
The In term is the quantity that is added to the circuit. This is the amount of power supplied by the voltage source and is equal to the voltage by the current (P=VI). The quantity that is removed (Out) is the amount of power removed by the circuit which is due to the resistor in this case and is equal to the resistance by the current squared (P=I2R). The accumulation is the buildup of electrical charge on the capacitor is equal to the voltage across the capacitor by the current (I x Vc = I x q/C).
The equation therefore becomes:
![]()
Dividing across by I gives:
![]()
The current I is equal to the rate of change of charge q, i.e. I = dq/dt. Therefore:
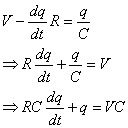
i.e. a first order differential equation where V is the input to the system and q is the output from the system.
Option 2 – Output is voltage across the capacitor
Another way of writing this equation is in terms of Vc, the voltage across the capacitor, instead of in terms of q. Vc is equal to the charge on the capacitor divided by the capacitance, i.e. Vc = q/C. Therefore:
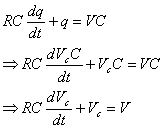
Another way of deriving this relationship is to use circuit analysis as follows:
![]()
where V is the applied voltage, VR is the voltage across the resistor and VC is the voltage across the capacitor. Since VR=IR, the equation can be rewritten as follows:
![]()
Now, the current I, is the rate at which charge moves to or from the capacitor plates, i.e. I = dq/dt. Also, the charge, q = VCxC. Therefore, the equation becomes:
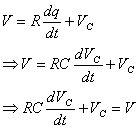
which is the same equation as above.
Either way, the equation is that of a first order type system where the time constant, t = RC and the static gain, K = 1.
The equation is converted to the frequency domain as follows:
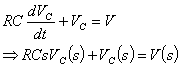
This is now easily modified to give the transfer function as follows:

Setting the input to the circuit to a step type (i.e. V = a ÞV(s) = a/s) gives the following:
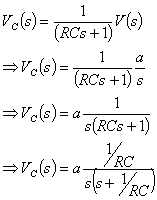
Having applied the step input and rearranged the equation in the frequency domain, we are now ready to transform back to the time domain. Checking the Laplace transform tables, a frequency domain function of the type b/s(s+b) has a time domain equivalent of (1-e-bt). In the equation above, b = 1/RC, therefore:
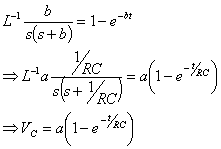
This equation describes the change in voltage across the capacitor when a step input voltage of a Volts is applied to the circuit.