Batch Distillation – No Reflux – Rayleigh Equation

In some cases a batch is heated and the vapour formed is removed immediately from the system without any reflux. This was analysed by Rayleigh. Assume that the still is charged with n_o mols of a mixture that has a liquid mol fraction of x_o for the MVC. The no. of mols in the still and the mol fractions at times t and t+dt are shown in the table below:

	Start	Time t	Time t+dt
Still (kmol)	no	n	n – dn
Mol fraction of comp A	xo	x	x – dx

x, y are the mol fractions of A (MVC) in the liquid and vapour.

A mass balance on the MVC gives:

MVC in still at time t = MVC in still + MVC removed as vapour in time t+dt

Using the symbols in the table, this reads as:

Ignoring second order differentials we get:

Rearrange the equation as follows:

This can be integrated. The limits for the integral are from time t=0 to time t. At t=0 we had n_o moles and a mol fraction x_o. At time t, we have n moles and a mol fraction of x. The limits of the integrals are swapped so the initial limit appears on top. This is to avoid a negative as there is less material at the end than at the start. The equation becomes:

The right hand side can be solved if the relationship between y and x is known. The relationship between y and x is given by the VLE data, i.e. the equilibrium curve. One option is to use the relative volatility relationship between y and x and integrate. The other option is to use a graphical method for integration.

Option 1 – Mathematical Integration

We need a relationship between y and x. Relative volatility is related to y and x by the following equation:

Add this into the integral and integrate between x and x_o to get:

Enter the numbers to get an answer for ln(n_o/n).

Option 2 – Graphical Integration

The graphical method is as follows:

1. From the x-y data plot x versus 1/(y-x) on graph paper or excel (easier!).

2. Draw vertical lines at the limits x_o and x

3. Determine the area enclosed by counting the number of squares. This is equal to ln(n_o/n).

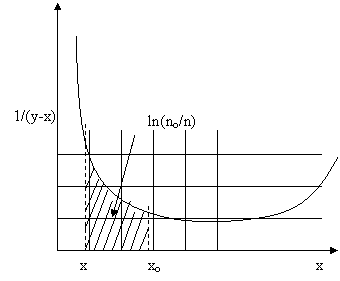
In this case there are approximately three whole squares and two ½ squares to give a total of 4 squares. Don’t forget that this is an area that depends on the size of your square. If the x-axis is notched at intervals of 0.1 and the y-axis is notched at intervals of 1, then the area of one square is 1x0.1=0.1. Therefore, 4 squares gives a total area of 0.4 so ln(n_o/n) = 0.4.

You now have ln(n_o/n). n_o is the total number of moles of everything in the still initially. Now you can get n, the number of moles left after distillation. Multiply n by the mol fraction you used to get ln(n_o/n) to give the number of moles of the MVC left.

With the Rayleigh equation we can determine what has happened in the still if we know what went into it in the first place and we choose a final mol fraction of the MVC in the still.