Dynamic Performance

This is a measure of how well a system responds to a changing input. The dynamic specification can be defined by applying one or all of three different inputs and examining the resultant output.

The Step or Transient Response comes from the Step Input. The Ramp Response is given by the Ramp input and the Frequency Response is produced by the Sine Wave Input.

Zero Order Systems are defined as follows. The output of a zero order system is proportional to the input. At all times, the output is equal to the input multiplied by some constant of proportionality.

Output qo = k x Input qi

qo = kqi

Where k is a proportionality constant.

Example – rheostat, potentiometer. The voltage/resistance (output) instantly changes when the wiper is moved (input).

First Order Systems ultimately reach the same result as zero order systems except that they take some time to get there when a step input is applied.

The relationship between the output and the input is given by the following equation:

where a, b and c are constants.

This equation is normally written as follows:

where t=a/b and is the time constant in seconds

K=c/b and is the static sensitivity (units depending on application)

The form of the step response is shown as follows:

The above curve is an exponential rise to a final value. The equation that relates the output to time is as follows:

where q_initial is the steady state value before the step input is applied and q_final is the steady state value after the step input is applied, i.e. after the exponential rise.

The time constant, t, is the length of time for the output to reach 63.2% of its final value. It takes almost five time constants for the output to reach its final value.

Thermometer example

Example. A thermocouple housed in a protective sheath has an output voltage of q_out Volts and an input temperature of q_in°C. Determine the time constant and the static sensitivity for this system if its dynamic performance is given by the following equation:

Solution. This equation is of the form given above. Rearranging slightly to give a unity coefficient for the q_out term gives the following equation:

This is of the form:

Therefore, the time constant t=10 and the static sensitivity k=0.5x10^-5.

Example. A pressure transducer which has a first order characteristic has pressures applied at the times shown in the following table:

Pressure (psi)	Time (sec)
10	0
20	5
35	8
12	12

If the time constant of the device is 6 seconds, what is the pressure recorded at the end of each time interval and sketch the approximate relationship between pressure and time over 15 seconds. The initial pressure is 0 psi.

Solution: The equation to use is, from above:

This is easily calculated and plotted using excel. Construct a spreadsheet as follows:

Time, t (sec)	Dt	Applied Pressure	Calculation	Output Pressure
0	-	10	-	0
5	5	20	0+(10-0)(1-exp(-5/6))	5.65
8	3	35	5.65+(20-5.65)(1-exp(-3/6))	11.30
12	4	12	11.3+(35-11.3)(1-exp(-4/6))	22.83
15	3	12	22.83+(12-22.83)(1-exp(-3/6))	18.57

Add in some extra rows with extra times and calculations to improve the chart.

Note that for this example the output pressure never has enough time to reach the applied pressure because of the value of the time constant. Try changing the time constant to 1.5seconds and see what happens to the chart (easily done in excel).

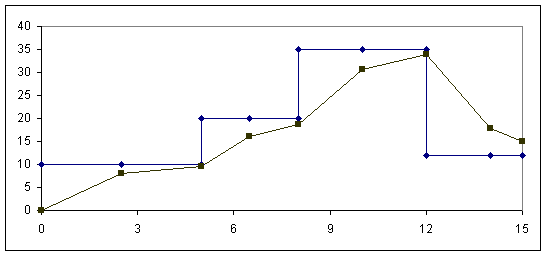
The output pressure almost reaches the applied pressure before it is changed. Remember, five time constants are needed to reach the applied pressure.

The frequency response of a first order system is obtained by applying sine waves of known amplitude at the input and examining the output response.

Bandwidth

Second order systems are defined by a second order differential equation. They can be underdamped leading to overshoot; they can be critically damped in which case the transient response looks like that of a first order system; or they can be overdamped resulting in sluggish behaviour without overshoot.